五度圏（cycle of 5th）を覚えて使い倒そう！　調号も平行調もコードもすぐ分かる

五度圏（サイクル・オブ・フィフス＝cycle of 5th）て何だかわかりますか？
これを覚えておくと、とても便利なんです。

これが五度圏

これの何が便利なのか。どうしてこのような図があるのか、説明していきますね。

まず五度（５ｔｈ）とは何かについて。
そもそも音楽における”度”とは、
『ある音とある音がどのくらい離れているか』
つまり、音程の差を表す時に”度”という表現を使います。
しかし、音楽で使う”度”が少しややこしいのは、
速度や温度、角度のように１度の差（幅）が一定ではないということ。
どういうことかというと、
短何度、長何度、増何度　減何度、完全何度と”度”にも色々な種類が存在するのです。
具体的には下記リンク先の”音楽の度はドーナツのド？”を見てください。

リンク：音楽の度はドーナツのド？

また、起点となる音（数え始めの音）はゼロではなく”１度”となります。

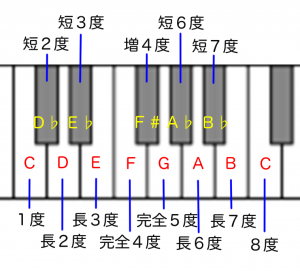
Ｃ（＝ド＝ハ）を起点にすると、
１オクターブ内には１２音（１２個の鍵盤）があり、
１３音目で１オクターブ上のＣになります。

１度＝Ｃ
短２度＝Ｄ♭
長２度＝Ｄ
短３度＝Ｅ♭
長３度＝Ｅ
完全４度＝Ｆ
増４度＝Ｆ＃・・・（減５度＝Ｇ♭）
完全５度＝Ｇ
短６度＝Ａ♭・・・（増５度＝Ｇ＃）
長６度＝Ａ
短７度＝Ｂ♭
長７度＝Ｂ
８度＝Ｃ（オクターブ）

同じようにＥ♭を起点にすると

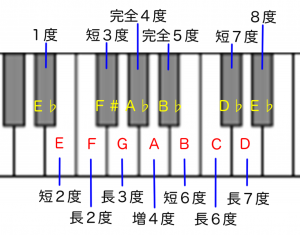
のようになります。
これは他の音を起点にした場合も、その起点の音を１度とし、
半音上がるごとに同様の度の並びとなります。
冒頭の五度とな何か、は、
この１２音で構成される音の中の完全５度となる音のことです。
五度圏とは、
起点となる音とその完全５度の音を３０°の角度で円上に（通常は時計回りに）記したもの。
Ｃを頂点（１２時の位置と）とし、Ｃの完全５度となるＧを３０°（１時の位置）に、
Ｇの完全５度となるＤをさらに３０°（２時の位置）に、
Ｄの完全５度となるＡをさらに３０°（３時の位置）に・・・と順に記して頂点のＣに戻ります。
この時、時計回りに１つ（３０°）進むと調号の＃が１つずつ増えていきます。
Ｃから反時計周りに１つ進むと調号の♭が１つずつ増えていきます。
１８０°（６時）の位置で＃と♭が入れ替わりますが、その前後を含めた３音では、
曲によって＃と♭の両方の記載方法があります。
※黒鍵は５個しかないのに＃や♭が６つになってますが、
通常”シ”として弾く白鍵を”ド♭”としたり、
通常”ファ”として弾く白鍵を”ミ＃”として扱います。
起点となる音とスケール上の各音の間隔（インターバル）の規則性からそのように扱います。

さて、長くなりましたが、５度圏のこの図の成り立ち（構造）はわかったと思います。
では、この図は何の役にたつのか。これが一番知りたいことですよね。

一番わかりやすいのが平行調が一目瞭然であるということ。
平行調とは、調号が同じになるメジャー（長調）とマイナー（短調）のこと。
Ｃメジャー（ハ長調）は調号に＃も♭もなく、スケールは白鍵のみのドレミファソラシドです。
この平行調がＡマイナー（イ短調）です。
起点となる音がＡ（＝ラ＝イ）となりますが、スケールは白鍵のみのラシドレミファソラです。
（マイナースケールには３種類あるが、ここでは特に記載がない場合ナチュラルマイナーとする）
この平行調の関係は５度圏の９０°の位置関係になっています。
具体的には、ある音をメジャーとすると、
そこから時計回りに９０°の位置にある音がマイナーの平行調です。
もちろん逆に、ある音がマイナーの場合、
反時計回りに９０°の位置にある音がメジャーの平行調です。
Ｃメジャー／Ａマイナー以外、５度圏を覚えていれば、
Ｂ♭メジャー／Ｇマイナー（調号♭２つ）とか、
Ａメジャー／Ｆ＃マイナー（調号＃３つ）などがすぐわかります。

平行調だけなら、わざわざ５度圏で確認しなくても
スケール練習を通じて自然と覚えられそうだけど、
他に役立つことはないのでしょうか。

３０°進むと５度の音。では６０°進むと？
音楽の度は起点が１度なので、４度上がります。
つまり５＋４で９度の音。９０°はさらに４度上がるので９＋４で１３度の音。
１２０°では１３＋４で１７度？
１オクターブは８度なので、８度と１度は同じ音に戻ります。なので８度以上は７を引いて
９度は２度、１３度は６度、１７度から７を引くと１０度、さらに７を引くと３度。
同様に１５０°は１７＋４で２１度、これらから１４引くと７度です。
１８０°は２１＋４で２５度、１４引くと１１度、さらに７引くと４度です。
つまり起点の音が１度でこれをルートとして３０°進んだ度を並べると１５２６３７４。
ひとつ跳びに１２３４と５６７になってます。
さらに進んでみましょう。
２１０度は２５＋４で２９度。２１を引くと８度？さらに７を弾いたら１度？
例えば起点の音がＣなら２１０°の位置はＤ♭またはＣ＃なので１度ではないですよね。
そういえば、１８０°の時も４度ってしたけど、
Ｇ♭（Ｆ＃）って４度じゃなくて、増４度（減５度）の音ですよね。
とりあえずこの疑問は一旦置いといて・・・
今度は３０°戻ってみましょう。
３０°戻る（反時計周りに進む）と４度進みます。
先ほどと同様に他の角度も計算すると、
６０°は４＋３で７度、９０°は３度（１０度）、１２０°は６度（１３度）、
１５０°は２度（９、１６度）、そして１８０°は５度（１２、１９度）。
計算した度と５度圏上の音は３０°の時の４度しか一致しないですね・・・
ただし、１８０°はどちら周りでも増４度/減５度で同じ結果になってます。

くどくどと計算してきましたが、実はこれ、どうでも良かったのです（ごめんなさい）。

気づいたかもしれませんが、音階の構成音は１２個で決まっているので、
５度圏にすべての構成音があります。
ここで、コード（和音）を考えてみましょう。
コード名が”Ｃ”の構成音は１度＝ルートＣ、長３度＝Ｅ、完全５度＝Ｇの
ドミソなのはすぐ分かると思います。
Ｃ７なら、このドミソに短７度＝Ｂ♭を加えたドミソシ♭。
Ｃｍ７なら長３度を短３度に置き換えてドミ♭ソシ♭。
ＣＭ７ならＣのドミソに長７度＝Ｂを加えてドミソシ。
つまり、
Ｃ＝１度＋長３度＋完全５度
Ｃ７＝１度＋長３度＋完全５度＋短７度
Ｃｍ７＝１度＋短３度＋完全５度＋短７度
ＣＭ７＝１度＋長３度＋完全５度＋長７度
です。
では、Ｂ♭ｍ７はどうでしょう。
Ｂ♭ｍ７はＢ♭-Ｄ♭-Ｆ-Ａ♭（シ♭-レ♭-ファ-ラ♭）です。
”度”で表すと、Ｂ♭（シ♭）が基準の１度（ルート）となり、
Ｂ♭ｍ７＝１度＋短３度＋完全５度＋短７度
と、Ｃｍ７と同じになります。
そんなことは知ってるかもしれませんが、次のような見方をしたら、あることに気付きませんか？

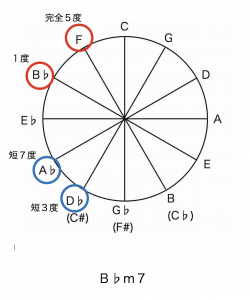
ではもう１つ。Ｃdimはどうなるのでしょうか。
ルート（１度）から短３度を積み上げていくとdimになります。
なので、Ｃdimは１度Ｃ（ド）、短３度はＥ♭（ミ♭）、Ｅ♭から短３度でＧ♭（ソ♭）、
さらにＧ♭から短３度のＡ（ラ）となります。ちなみにＡの短３度はＣになります。
これを全部Ｃを起点に度で表すと
Ｃdim＝１度＋短３度＋減５度＋長６度
となります。５度圏に記してみましょう。

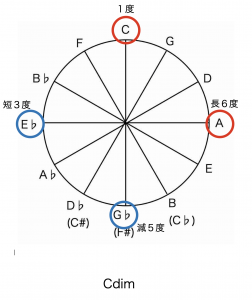
これを見るとdimコードの構成音は５度圏の９０°ずつ離れた音となっています。
ＡdimもＧ♭dimもＥ♭dimも全てＣdimと構成音が同じということです。
そして、Ｃから３０°のＧdimのグループと６０°のＤdimのグループの
３種類に集約されることが５度圏の図から分かるのです。

Ｃを起点にして、５度圏の図と”度”の関係はどうなっているのでしょうか。

この５度圏の図から、Ｃにとって他の音が何度なのかわかります。
起点となる音（ルート）から時計回りに１-完５-長２-長６-長３-長７増４。
反時計回りに１-完４-短７-短３-短６-短２-減５となってます。
１度両側は完全５度、完全４度、１８０°は増４度／減５度。
時計回りは長音、反時計回りは短音。
ここで、先ほどグダグダと計算してた一見ムダだった話を思い出してみましょう。
そうです、一つ跳びに見ると時計回りは１−２−３−４、５−６−７。
反時計回りは１（＝８）-７-６-５、４-３-２。
となっているのです。これなら覚えるの簡単ですよね。

たとえば、ＣＭ７なら１度-長３度-完全５度-長７度であるため、この図より
ＣＭ７＝Ｃ＋Ｅ＋Ｇ＋Ｂであることが分かります。

これは、１度をＣから他の５度圏上の音に移動した場合には、
赤文字の各”度”の部分も一緒に回っていきます。
１度をＦにすれば完全５度はＣの位置にきます。
これは、コードの種類ごとに５度圏に構成音のパターンがあり、ルートが決まれば、
そこを起点に５度圏におけるコードパターンを当てはめれば、
そのコードの構成音がすぐに分かるのです。
もちろん、コード理論の知識があれば５度圏に頼る必要はないし、
鍵盤のイラストを使ったコード一覧のようなものもあります。
でも、ボーカル曲などで伴奏する場合に移調することがよくありますが、
５度圏を使ったら簡単にコードの置き換えができるんです。

まとめ

５度圏の図から平行調がすぐにわかるだけでなく、コードの構成音もすぐ分かる。

『５度圏の音の位置（CGDAEBG♭D♭A♭E♭B♭F）と
一つ跳びに時計回りは長、１２３４、５６７、
反時計回りは短、８７６５、４３２、
１度の隣りは完全、１８０°は増減。』

あとは、Cをルートに各種コードのパターンを覚える。
たったこれだけです！！

よく使うコードは、ｍ、ｍ７、M7、ｍ７−5（＝φ／ハーフディミニッシュ）、
dim、aug、sus4くらいでしょうか。
ちなみにジャズといえばテンションですが、９度１１度１３度は２度４度６度のオクターブ違い。
なので、テンションノートがどの音になるかも、この５度圏で分かるのです。
なお、＃９thは短３度のオクワーブ違いです、念のため。

【参照リンク】５度圏コードパターン　Ｃコード一覧